Rooty helix

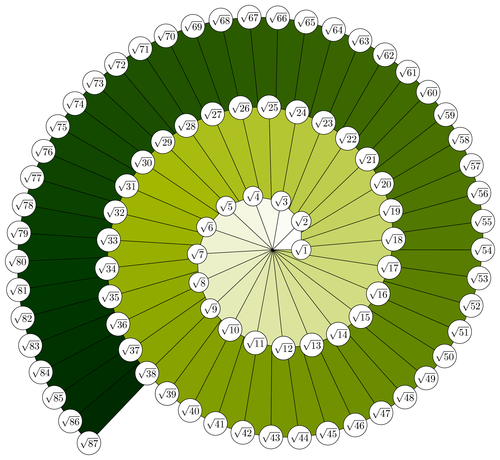
The idea of the rooty-helix is very simple. One starts e.g. with the length of 1, adds a right angle with the length of 1 and the hypotenuse equals sqrt{2}. If one continues with sqrt{2} repeating the procedure (adding a right angle with the length of 1) the hypotenuse is sqrt{3}. And so on and so on. At some point due to the iterations some triangles are overpainted. Because of this, one repaints the overpainted triangles

Edit and compile if you like:

% Rooty helix
% Author: Felix Lindemann
\documentclass{minimal}

\usepackage{tikz}
\usetikzlibrary{calc}


\begin{document}

\pagestyle{empty}
\pgfdeclarelayer{background}
\pgfdeclarelayer{foreground}
\pgfsetlayers{background,main,foreground}

\xdefinecolor{darkgreen}{RGB}{175, 193, 36}
\newcounter{cntShader}
\newcounter{cntRoot}
\setcounter{cntShader}{20}
\def\couleur{darkgreen}

\begin{tikzpicture}
    \foreach \y in {86,38,15}{
        \setcounter{cntShader}{1}
        \coordinate (a) at (0,0);
        \coordinate (b) at (0:1);
        \foreach \x in {1,...,\y}{%
            \coordinate (c) at ($ (b)!1cm!270:(a) $);
            \begin{pgfonlayer}{background}
                \draw[fill=\couleur!\thecntShader] (a)--(b)--(c)--cycle;
            \end{pgfonlayer}
            \setcounter{cntRoot}{\x}
            \addtocounter{cntRoot}{1}
            \node[fill=white,draw,circle,inner sep=1pt] at (c)
                {$\sqrt{\thecntRoot}$};
            \coordinate (b) at (c);
            \pgfmathsetcounter{cntShader}{\thecntShader+4}
            \setcounter{cntShader}{\thecntShader}
       }
    }
    \node[fill=white,draw,circle,inner sep=1pt] at (0:1) {$\sqrt{1}$};
\end{tikzpicture}

\end{document}