Prim’s algorithm

A step by step example of the Prim's algorithm for finding the minimum spanning tree. Animated using Beamer overlays.

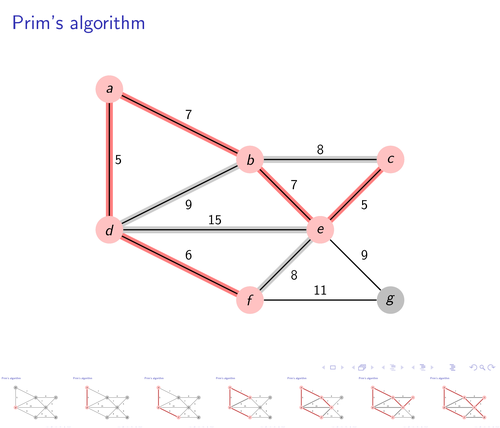
Edit and compile if you like:

\documentclass{beamer}

\usepackage{tikz}

\usetikzlibrary{arrows,shapes}


\begin{document}

% Declare layers
\pgfdeclarelayer{background}
\pgfsetlayers{background,main}

\begin{frame}
\frametitle{Prim's algorithm}

%% Adjacency matrix of graph
%% \  a  b  c  d  e  f  g
%% a  x  7     5
%% b  7  x  8  9  7
%% c     8  x     5
%% d  5  9     x 15  6
%% e     7  5 15  x  8  9
%% f           6  8  x 11
%% g              9  11 x

\tikzstyle{vertex}=[circle,fill=black!25,minimum size=20pt,inner sep=0pt]
\tikzstyle{selected vertex} = [vertex, fill=red!24]
\tikzstyle{edge} = [draw,thick,-]
\tikzstyle{weight} = [font=\small]
\tikzstyle{selected edge} = [draw,line width=5pt,-,red!50]
\tikzstyle{ignored edge} = [draw,line width=5pt,-,black!20]

\begin{figure}
\begin{tikzpicture}[scale=1.8, auto,swap]
    % Draw a 7,11 network
    % First we draw the vertices
    \foreach \pos/\name in {{(0,2)/a}, {(2,1)/b}, {(4,1)/c},
                            {(0,0)/d}, {(3,0)/e}, {(2,-1)/f}, {(4,-1)/g}}
        \node[vertex] (\name) at \pos {$\name$};
    % Connect vertices with edges and draw weights
    \foreach \source/ \dest /\weight in {b/a/7, c/b/8,d/a/5,d/b/9,
                                         e/b/7, e/c/5,e/d/15,
                                         f/d/6,f/e/8,
                                         g/e/9,g/f/11}
        \path[edge] (\source) -- node[weight] {$\weight$} (\dest);
    % Start animating the vertex and edge selection. 
    \foreach \vertex / \fr in {d/1,a/2,f/3,b/4,e/5,c/6,g/7}
        \path<\fr-> node[selected vertex] at (\vertex) {$\vertex$};
    % For convenience we use a background layer to highlight edges
    % This way we don't have to worry about the highlighting covering
    % weight labels. 
    \begin{pgfonlayer}{background}
        \pause
        \foreach \source / \dest in {d/a,d/f,a/b,b/e,e/c,e/g}
            \path<+->[selected edge] (\source.center) -- (\dest.center);
        \foreach \source / \dest / \fr in {d/b/4,d/e/5,e/f/5,b/c/6,f/g/7}
            \path<\fr->[ignored edge] (\source.center) -- (\dest.center);
    \end{pgfonlayer}
\end{tikzpicture}
\end{figure}

\end{frame}

\end{document}