- In any triangle ABC, there exists a circle passing through nine special points :
- the 3 middles of sides
- the 3 vertices projections on opposite sides
- the middles of segments [HA], [HB] and [HC] such that H is the intersection point of the 3 altitudes
This TikZ code shows these points.
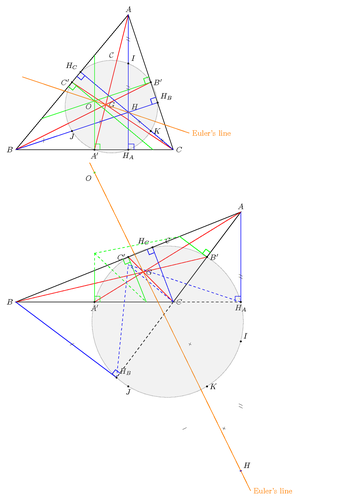
Edit and compile if you like:
% Nine points circle of a triangle
% Author : Arnaud Lefebvre (IREM Rouen)
%
% In any triangle ABC, there exists a circle passing through
% nine special points :
% - the 3 middles of sides
% - the 3 vertices projections on opposite sides
% - the middles of segments [HA], [HB] and [HC] such that
% H is the intersection point of the 3 altitudes
% Requirements :
% - tkz-2d.sty
% - tkz-arith.sty
% - tkz-base.sty
% - tkz-berge.sty
% - developement version of PGF
\documentclass{article}
\usepackage[active,tightpage]{preview}
\PreviewEnvironment{tikzpicture}
\setlength\PreviewBorder{5pt}%
\usepackage{tikz,tkz-2d}
\usetikzlibrary{calc,through,intersections}
\usepackage{ifthen}
\usepackage{geometry}
\geometry{vmargin=1cm}
% Definition of the command showing the nine points
\newcommand\ninepointscircle[3]{%
\begin{tikzpicture}
%----------------------------------------------------------
% Vertices of the triangle
%----------------------------------------------------------
\coordinate[label=above:$A$] (A) at (#1);
\coordinate[label=left:$B$] (B) at (#2);
\coordinate[label=right:$C$] (C) at (#3);
%----------------------------------------------------------
% Middles of sides
%----------------------------------------------------------
\coordinate[label=below:$A'$] (A') at ($(B)!.5!(C)$);
\coordinate[label=right:$B'$] (B') at ($(A)!.5!(C)$);
\coordinate[label=left:$C'$] (C') at ($(B)!.5!(A)$);
%----------------------------------------------------------
% Projections of vertices on opposite sides
%----------------------------------------------------------
\coordinate[label=below:$H_A$] (HA) at ($(B)!(A)!(C)$);
\coordinate[label=45:$H_B$] (HB) at ($(A)!(B)!(C)$);
\coordinate[label=135:$H_C$] (HC) at ($(B)!(C)!(A)$);
%----------------------------------------------------------
% Drawing the triangle, medians and altitudes
%----------------------------------------------------------
\draw[name path=triangle] (A) -- (B) -- (C) -- cycle;
\draw[color=red,name path=ma] (A)--(A');
\draw[color=red,name path=mb] (B)--(B');
\draw[color=red,name path=mc] (C)--(C');
\draw[fill=blue,color=blue,name path=ha] (A) -- (HA);
\draw[fill=blue,color=blue,name path=hb] (B) -- (HB);
\draw[fill=blue,color=blue,name path=hc] (C) -- (HC);
\tkzRightAngle[color=blue](B/HC/C,C/HA/A,A/HB/B)
%----------------------------------------------------------
% Drawing perpendicular bisectors
%----------------------------------------------------------
\tkzMathLength(A,HA)
\path [name path=C1] (A') -- ($(A')!\tkzMathLen pt!90:(C)$);
\tkzMathLength(B,HB)
\path [name path=C2] (B') -- ($(B')!\tkzMathLen pt!90:(A)$);
\tkzMathLength(C,HC)
\path [name path=C3] (C') -- ($(C')!\tkzMathLen pt!90:(B)$);
\draw[color=green,name intersections={of=triangle and C1,name=ch1,sort by=C1,total=\t}]
(ch1-\t)--(A') coordinate (OA') at (ch1-\t);
\draw[color=green,name intersections={of=triangle and C2,name=ch2,sort by=C2,total=\t}]
(ch2-\t)--(B') coordinate (OB') at (ch2-\t);
\draw[color=green,name intersections={of=triangle and C3,name=ch3,sort by=C3,total=\t}]
(ch3-\t)--(C') coordinate (OC') at (ch3-\t);
%----------------------------------------------------------
% Drawing angles
%----------------------------------------------------------
\tkzRightAngle[color=green](B/C'/OC',C/A'/OA',A/B'/OB')
%----------------------------------------------------------
% Drawing in dashed style in case of obtuse angle
%----------------------------------------------------------
\tkzMathLength(B,C)
\ifthenelse{\isundefined{\la}}{\newlength{\la}}{}
\setlength{\la}{\tkzMathLen pt}
\setlength{\la}{.01\la}
\tkzMathLength(A,C)
\ifthenelse{\isundefined{\lb}}{\newlength{\lb}}{}
\setlength{\lb}{\tkzMathLen pt}
\setlength{\lb}{.01\lb}
\tkzMathLength(A,B)
\ifthenelse{\isundefined{\lc}}{\newlength{\lc}}{}
\setlength{\lc}{\tkzMathLen pt}
\setlength{\lc}{.01\lc}
\pgfmathsetmacro{\angle}{acos((\la*\la-\lb*\lb-\lc*\lc)/(-2*\lb*\lc))}
\pgfmathtruncatemacro\A{\angle}
\ifthenelse{\A>90}{
\draw[style=dashed,color=green] (O)--(OA') (O)--(OB') (O)--(OC');
\draw [style=dashed, color=black] (A)--(HC) (A)--(HB);
\draw[style=dashed,color=blue] (A)--(H) (HB)--(H) (HC)--(H);}{}
\pgfmathsetmacro{\angle}{acos((\lb*\lb-\la*\la-\lc*\lc)/(-2*\la*\lc))}
\pgfmathtruncatemacro\B{\angle}
\ifthenelse{\B>90}{
\draw[style=dashed,color=green] (O)--(OA') (O)--(OB') (O)--(OC');
\draw [style=dashed, color=black] (B)--(HA) (B)--(HC);
\draw[style=dashed,color=blue] (B)--(H) (HC)--(H) (HA)--(H);}{}
\pgfmathsetmacro{\angle}{acos((\lc*\lc-\la*\la-\lb*\lb)/(-2*\lb*\la))}
\pgfmathtruncatemacro\C{\angle}
\ifthenelse{\C>90}{
\draw[style=dashed,color=green] (O)--(OA') (O)--(OB') (O)--(OC');
\draw [style=dashed, color=black] (C)--(HA) (C)--(HB);
\draw[style=dashed,color=blue] (C)--(H) (HB)--(H) (HA)--(H);}{}
%----------------------------------------------------------
% Positioning gravity center, centroid, circumcenter
% and the nine points circle center
%----------------------------------------------------------
\coordinate[label=45:$H$] (H) at (intersection of A--HA and B--HB);
\coordinate[label=0:$G$] (G) at (intersection of A--A' and B--B');
\coordinate[label=-135:$O$] (O) at (intersection of OC'--C' and OB'--B');
\draw[fill=red,color=red] (G) circle (.8pt);
\draw[fill=blue,color=blue] (H) circle (.8pt);
\draw[fill=green,color=green] (O) circle (.8pt);
\coordinate (N) at ($(H)!.5!(O)$);
%----------------------------------------------------------
% Drawing the Euler's line (also in case of obtuse angle)
%----------------------------------------------------------
\ifthenelse{\la>\lb}{\def\m{max(\la,\lc)}}{\def\m{max(\lb,\lc)}}
\ifthenelse{\A>90}{\draw[color=orange] (G)--($(G)!1.1!(O)$) (G)--($(G)!1.1!(H)$) node[right]{Euler's line};}{
\ifthenelse{\B>90}{\draw[color=orange] (G)--($(G)!1.1!(O)$) (G)--($(G)!1.1!(H)$) node[right]{Euler's line};}{
\ifthenelse{\C>90}{\draw[color=orange] (G)--($(G)!1.1!(O)$) (G)--($(G)!1.1!(H)$) node[right]{Euler's line};}{
\draw[color=orange] (G)--($(G)!50*\m!(O)$) (G)--($(G)!50*\m!(H)$) node[right]{Euler's line};}}}
%----------------------------------------------------------
% Marking points of interest
%----------------------------------------------------------
\draw[fill=black] ($(A)!.5!(H)$) circle (.8pt) node[anchor=south west] {$I$};
\path ($(A)!.5!(H)$) -- node[sloped] {\tiny{//}} (A);
\path ($(A)!.5!(H)$) -- node[sloped] {\tiny{//}} (H);
\draw[fill=black] ($(B)!.5!(H)$) circle (.8pt) node[below] {$J$};
\path ($(B)!.5!(H)$) -- node[sloped] {\tiny{/}} (B);
\path ($(B)!.5!(H)$) -- node[sloped] {\tiny{/}} (H);
\draw[fill=black] ($(C)!.5!(H)$) circle (.8pt) node[right] {$K$};
\path ($(C)!.5!(H)$) -- node[sloped] {\tiny{$\times$}} (C);
\path ($(C)!.5!(H)$) -- node[sloped] {\tiny{$\times$}} (H);
\draw[fill=black] (A') circle (.8pt);
\draw[fill=black] (B') circle (.8pt);
\draw[fill=black] (C') circle (.8pt);
\draw[fill=black] (HA) circle (.8pt);
\draw[fill=black] (HB) circle (.8pt);
\draw[fill=black] (HC) circle (.8pt);
%----------------------------------------------------------
% Drawing the nine points circle
%----------------------------------------------------------
\node[fill=lightgray,opacity=.2,draw,circle through=(C'),
label=90:$\mathcal{C}$] at (N) {};
\end{tikzpicture}
}
\begin{document}
\pagestyle{empty}
\begin{preview}
\ninepointscircle{5,6}{0,0}{7,0}\\
\ninepointscircle{10,4}{0,0}{7,0}
\end{preview}
\end{document}
Click to download: nine-points-circle-of-a-triangle.tex • nine-points-circle-of-a-triangle.pdf
Open in Overleaf: nine-points-circle-of-a-triangle.tex