Morley’s triangle

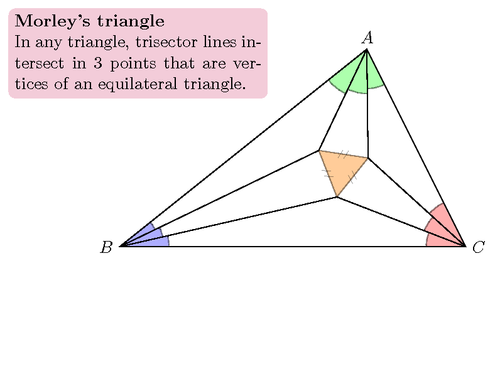
In any triangle, trisector lines intersect in 3 points that are vertices of an equilateral triangle.

Note that this example requires the tkz-2d package.

Edit and compile if you like:

% Morley's triangle
% Author : Arnaud Lefebvre (IREM Rouen)
% Intersections of trisector lines in any triangle
% are vertices of an equilateral triangle

\documentclass{article}

\usepackage{tikz,tkz-2d}
\usepackage[active,tightpage]{preview}
\PreviewEnvironment{tikzpicture}
\setlength\PreviewBorder{5pt}%

\usetikzlibrary{calc,intersections}

\pagestyle{empty}

\begin{document}

\begin{tikzpicture}

%----------------------------------------------------
% Coordinates of A, B and C, the triangle vertices 
%----------------------------------------------------
\coordinate[label=above:$A$] (A) at (5,4);
\coordinate[label=left:$B$] (B) at (0,0);
\coordinate[label=right:$C$] (C) at (7,0);

%----------------------------------------------------
% Lengths of segments [AB], [BC], and [CA] 
%----------------------------------------------------
\tkzMathLength(B,C)
\newlength{\la}
\setlength{\la}{\tkzMathLen pt}
\setlength{\la}{.01\la}
\tkzMathLength(A,C)
\newlength{\lb}
\setlength{\lb}{\tkzMathLen pt}
\setlength{\lb}{.01\lb}
\tkzMathLength(A,B)
\newlength{\lc}
\setlength{\lc}{\tkzMathLen pt}
\setlength{\lc}{.01\lc}

%----------------------------------------------------
% Computing 1/3 of each angle
%----------------------------------------------------
\pgfmathsetmacro{\A}{acos((\la*\la-\lb*\lb-\lc*\lc)/(-2*\lb*\lc))};
\pgfmathsetmacro{\tA}{\A/3};
\pgfmathsetmacro{\B}{acos((\lb*\lb-\la*\la-\lc*\lc)/(-2*\la*\lc))};
\pgfmathsetmacro{\tB}{\B/3};
\pgfmathsetmacro{\C}{acos((\lc*\lc-\lb*\lb-\la*\la)/(-2*\lb*\la))};
\pgfmathsetmacro{\tC}{\C/3};

%----------------------------------------------------
% Computing intersections of trisector lines
%----------------------------------------------------
\coordinate (A1) at ($(A)!100*max(\lb,\lc)!\tA:(B)$);
\coordinate (A2) at ($(A)!100*max(\lb,\lc)!2*\tA:(B)$);
\coordinate (B1) at ($(B)!100*max(\la,\lc)!\tB:(C)$);
\coordinate (B2) at ($(B)!100*max(\la,\lc)!2*\tB:(C)$);
\coordinate (C1) at ($(C)!100*max(\la,\lb)!\tC:(A)$);
\coordinate (C2) at ($(C)!100*max(\la,\lb)!2*\tC:(A)$);

%----------------------------------------------------
% Computing coordinates of vertices O, P and Q of 
% the Morley's triangle 
%----------------------------------------------------
\coordinate (O) at (intersection of C--C1 and A--A2);
\coordinate (P) at (intersection of A--A1 and B--B2);
\coordinate (Q) at (intersection of B--B1 and C--C2);

%----------------------------------------------------
% Drawing triangles and trisectors
%----------------------------------------------------
\tkzMarkAngle[size=1,fillcolor=green!80](B/A/A1)
\tkzMarkAngle[size=.9,fillcolor=green!80](A2/A/A1)
\tkzMarkAngle[size=.8,fillcolor=green!80](A2/A/C)
\tkzMarkAngle[size=1,fillcolor=blue!80](C/B/B1)
\tkzMarkAngle[size=.9,fillcolor=blue!80](B2/B/B1)
\tkzMarkAngle[size=.8,fillcolor=blue!80](B2/B/A)
\tkzMarkAngle[size=1,fillcolor=red!80](A/C/C1)
\tkzMarkAngle[size=.9,fillcolor=red!80](C2/C/C1)
\tkzMarkAngle[size=.8,fillcolor=red!80](C2/C/B)
\draw (A)--(B)--(C)--cycle;
\draw[fill=orange, opacity=.4] 
   (O)--node[sloped]{\tiny{//}}
   (P)--node[sloped]{\tiny{//}}
   (Q)--node[sloped]{\tiny{//}}(O);
\draw (A)--(O) (A)--(P) (B)--(P) (B)--(Q) (C)--(Q) (C)--(O);

%----------------------------------------------------
% Caption
%----------------------------------------------------
\node[rounded corners, fill=purple!20,anchor=south east] at (3,3) 
   {\begin{minipage}{5cm}
     \textbf{Morley's triangle}\newline In any triangle, trisector 
     lines intersect in 3 points that are vertices of an 
     equilateral triangle.
   \end{minipage}};

\end{tikzpicture}

\end{document}