Genaille and Lucas sticks for multiplication and division

GL sticks provide an easy method to perform multiplications and divisions: just read the result...

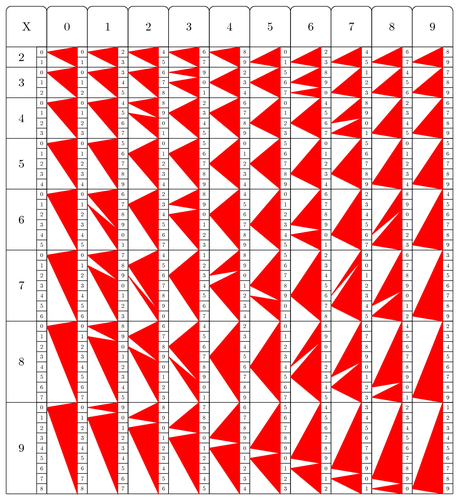
Edit and compile if you like:

% Genaille and Lucas sticks for multiplication and division
% Author : Arnaud Lefebvre (IREM Rouen)
% GL sticks provide an easy method to perform multiplications
% and divisions: just read the result... 

\documentclass{article}

\usepackage{tikz}
\usepackage[active,tightpage]{preview}
\PreviewEnvironment{tikzpicture}
\setlength\PreviewBorder{5pt}%


%-----------------------------------------------
% environment for drawing sticks 
% an option of the form scale=VALUE can be given
%------------------------------------------------
\newenvironment{sticks}[1][scale=.6]
 {\begin{tikzpicture}[#1]\def\W{0}\def\WS{0}}
 {\end{tikzpicture}}

%------------------------------------------------------------
% \stickME draws an empty multiplication stick 
%------------------------------------------------------------
\newcommand{\stickME}{%
 \begin{scope}[xshift=\W cm]
   \pgfmathparse{\W+2}
   \global\let\W\pgfmathresult
   \draw [black,rounded corners] (2,0) -- (2,24) -- (0,24) -- (0,0); 
   \draw (0,0) -- (2,0);
   \foreach \x in {.5,1,...,22} {
     \draw (1.5,\x) -- (2,\x);
   }
   \draw (1.5,0) -- (1.5,22);
   \foreach \x in {4.5,8.5,12,15,17.5,19.5,21,22} {
     \draw (0,\x) -- (2,\x);
   }
 \end{scope}
}

%--------------------------------------------------------
% \stickDE draws an empty division stick 
%--------------------------------------------------------
\newcommand{\stickDE}{%
 \begin{scope}[xshift=\W cm]
   \pgfmathparse{\W+2}
   \global\let\W\pgfmathresult
   \draw [black,rounded corners] (2,0) -- (2,24) -- (0,24) -- (0,0); 
   \draw (0,0) -- (2,0);
   \foreach \x in {.5,1,...,22} {
     \draw (0,\x) -- (.5,\x);
   }
   \draw (.5,0) -- (.5,22);
   \foreach \x in {4.5,8.5,12,15,17.5,19.5,21,22} {
     \draw (0,\x) -- (2,\x);
   }
 \end{scope}
}

%-------------------------------------------------------------
% \drawX draws the special X stick 
%-------------------------------------------------------------
\newcommand{\stickX}{%
 \stickME
 \begin{scope}[xshift=\WS cm]
   \pgfmathparse{\WS+2}
   \global\let\WS\pgfmathresult
   \node at (1,23) {X};
   \pgfmathparse{21.75}
   \global\let\z\pgfmathresult
   \pgfmathparse{21.5}
   \global\let\w\pgfmathresult
   \foreach \x in {2,3,4,5,6,7,8,9} {
     \node at (.75,\w) {\x};
     \pgfmathparse{\w-.75-.5*(\x-1)}
     \global\let\w\pgfmathresult
     \pgfmathparse{\x-1}
     \foreach \y in {0,...,\pgfmathresult} {
       \node[scale=.5] at (1.75,\z){\y}; 
       \pgfmathparse{-0.5+\z}
       \global\let\z\pgfmathresult
     }
   }
 \end{scope}
}

%-----------------------------------------------
% \stickR draws the special R stick 
%-----------------------------------------------
\newcommand{\stickR}{%
 \stickDE
 \begin{scope}[xshift=\WS cm]
   \pgfmathparse{\WS+2}
   \global\let\WS\pgfmathresult
   \node at (1,23) {R};
   \pgfmathparse{21.75}
   \global\let\z\pgfmathresult
   \pgfmathparse{21.5}
   \global\let\w\pgfmathresult
   \foreach \x in {2,3,4,5,6,7,8,9} {
     \node at (1.25,\w) {\x};
     \pgfmathparse{\w-.75-.5*(\x-1)}
     \global\let\w\pgfmathresult
     \pgfmathparse{\x-1}
     \foreach \y in {0,...,\pgfmathresult} {
       \node[scale=.5] at (.25,\z){\y}; 
       \pgfmathparse{-0.5+\z}
       \global\let\z\pgfmathresult
     }
   }
 \end{scope}
}

%------------------------------------------------------------------
% \stickM draws the stick of a multiplication table 
% #1 is the number of the table: value between 0 and 9
% #2 is the color of the triangles
%------------------------------------------------------------------
\newcommand{\stickM}[2]{%
 \stickME
 \begin{scope}[xshift=\WS cm]
   \pgfmathparse{\WS+2}
   \global\let\WS\pgfmathresult
   \node at (1,23) {#1};
   \pgfmathparse{21.75}
   \global\let\z\pgfmathresult
   \pgfmathparse{21.75}
   \global\let\w\pgfmathresult
   \foreach \x in {2,3,4,5,6,7,8,9} {
     \pgfmathparse{\x-1}
     \foreach \y in {0,...,\pgfmathresult} {
       \pgfmathmod{#1*\x+\y}{10}
       \pgfmathtruncatemacro\u\pgfmathresult
       \pgfmathtruncatemacro\d{(#1*\x+\y)/10}
       \node[scale=.5] at (1.75,\z){\u}; 
       \pgfmathparse{\z+.25}
       \let\a\pgfmathresult
       \pgfmathparse{\w-.5*\d}
       \let\b\pgfmathresult
       \pgfmathparse{\z-.25}
       \let\c\pgfmathresult
       \draw[color=#2, fill=#2, thin] (0,\b) -- (1.5,\a) -- (1.5,\c) -- (0,\b);
       \pgfmathparse{-0.5+\z}
       \global\let\z\pgfmathresult
     }
     \pgfmathparse{\w-\x*.5}
     \global\let\w\pgfmathresult
   }
 \end{scope}
}

%------------------------------------------------------------
% \stickD draws the stick of a division table 
% #1 is the number of the table: value between 0 and 9
% #2 is the color of the lines
%------------------------------------------------------------
\newcommand{\stickD}[2]{%
 \stickDE
 \begin{scope}[xshift=\WS cm]
   \pgfmathparse{\WS+2}
   \global\let\WS\pgfmathresult
   \node at (1,23) {#1};
   \pgfmathparse{21.75}
   \global\let\z\pgfmathresult
   \pgfmathparse{21.75}
   \global\let\w\pgfmathresult
   \foreach \x in {2,3,4,5,6,7,8,9} {
     \pgfmathparse{\x-1}
     \foreach \y in {0,...,\pgfmathresult} {
       \pgfmathtruncatemacro\q{(#1+10*\y)/\x}
       \node[scale=.5] at (.25,\z){\q}; 
       \pgfmathmod{#1+10*\y}{\x}
       \pgfmathparse{\w-.5*\pgfmathresult}
       \let\r\pgfmathresult
       \draw[color=#2] (.5,\z) -- (2,\r);
       \pgfmathparse{-0.5+\z}
       \global\let\z\pgfmathresult
     }
     \pgfmathparse{\w-\x*.5}
     \global\let\w\pgfmathresult
   }
 \end{scope}
}

\begin{document}
\pagestyle{empty}

% starting sticks environment
\begin{sticks}
  % drawing the special X stick
  \stickX
  % drawing the muliplication tables sticks in red 
  \stickM{0}{red}
  \stickM{1}{red}
  \stickM{2}{red}
  \stickM{3}{red}
  \stickM{4}{red}
  \stickM{5}{red}
  \stickM{6}{red}
  \stickM{7}{red}
  \stickM{8}{red}
  \stickM{9}{red}
\end{sticks}
% starting sticks environment
\begin{sticks}
  % drawing the division tables sticks in red 
  \stickD{0}{red}
  \stickD{1}{red}
  \stickD{2}{red}
  \stickD{3}{red}
  \stickD{4}{red}
  \stickD{5}{red}
  \stickD{6}{red}
  \stickD{7}{red}
  \stickD{8}{red}
  \stickD{9}{red}
  % drawing the special R stick
  \stickR
\end{sticks}
\end{document}