Combinatorial graphs

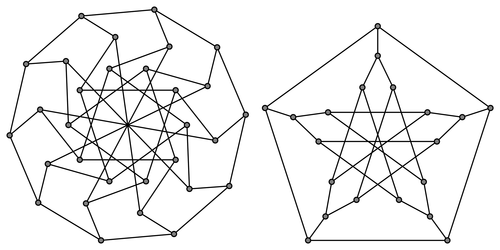
Two fascinating graphs from the very interesting Graph Theory in LaTeX gallery. The graphs are excellent examples of how flexible and powerful TikZ' path constructs are. See the source code for more details.

Update: Fixed an error in the code for drawing Tutte's 8-cage graph.

Edit and compile if you like:

% Combinatorial graphs
% Author: Rafael Villarroel
% Source: http://graphtheoryinlatex.blogspot.com/
\documentclass{article}
\usepackage{tikz}
\pagestyle{empty}


\begin{document}


% Define style for nodes
\tikzstyle{every node}=[circle, draw, fill=black!50,
                        inner sep=0pt, minimum width=4pt]
%  Tutte's 8-cage
\begin{tikzpicture}[thick,scale=0.8]
    % The following path utilizes several useful tricks and features:
    % 1) The foreach statement is put inside a path, so all the edges
    %    will in fact be a the same path.
    % 2) The node construct is used to draw the nodes. Nodes are special
    %    in the way that they are drawn *after* the path is drawn. This
    %    is very useful in this case because the nodes will be drawn on
    %    top of the path and therefore hide all edge joins.
    % 3) Simple arithmetics can be used when specifying coordinates.
    \draw \foreach \x in {0,36,...,324}
    {
        (\x:2) node {}  -- (\x+108:2)
        (\x-10:3) node {} -- (\x+5:4)
        (\x-10:3) -- (\x+36:2)
        (\x-10:3) --(\x+170:3)
        (\x+5:4) node {} -- (\x+41:4)
    };
\end{tikzpicture}\quad
%
%
% The largest 3-regular graph of diameter 3
\begin{tikzpicture}[thick,scale=0.8]%
    \draw \foreach \x in {18,90,...,306} {
        (\x:4) node{} -- (\x+72:4)
        (\x:4) -- (\x:3) node{}
        (\x:3) -- (\x+15:2) node{}
        (\x:3) -- (\x-15:2) node{}
        (\x+15:2) -- (\x+144-15:2)
        (\x-15:2) -- (\x+144+15:2)
};
\end{tikzpicture}


\end{document}