Archimedes’s approximation of pi

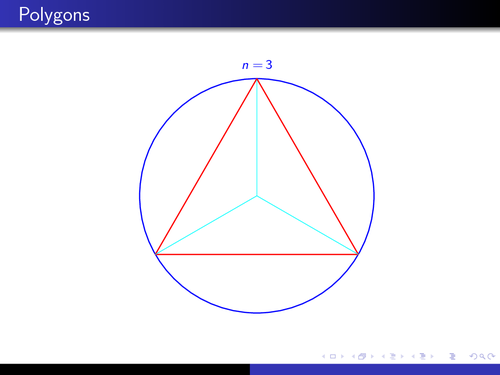
An animation of Archimedes's approximation of pi.

Edit and compile if you like:

% 
% Author:
% Efraín Soto Apolinar.
% www.aprendematematicas.org
%
% Animation to explain the approximation
% of $\pi$ as Archimedes did.
% 
\documentclass[spanish,10pt]{beamer}

\usepackage{color}
\usepackage{tikz}
\usepackage{animate}
\usepackage{calc}
%\usepackage{pgfmath}
%
\usepackage{hyperref}
\hypersetup{pdfpagemode=FullScreen}
% Beamer Settings
\usetheme{Warsaw}
% Counters
\newcounter{m} % Number of sides of the polygon
\setcounter{m}{2}
\newcounter{c} % Internal Control Counter
%
%
%
\begin{document}
%
%
%
\begin{frame}[fragile]{Polygons}
\begin{center}
\begin{animateinline}[loop, poster = first, controls, palindrome]{25}
\whiledo{\them<100}{
	\stepcounter{m}
	\setcounter{c}{0}
	%
	\begin{tikzpicture}[rotate=90]
	\draw[blue,thick] (0,0) circle (3cm); 
	% The polygons [Note: This is NOT the name of a band]
	\whiledo{\thec<\them}{
		\pgfmathparse{\thec*(360.0/\them)}
		\coordinate (initial) at (\pgfmathresult:3cm);
		%
		\pgfmathparse{(\thec+1)*(360.0/\them)}
		\coordinate (final) at (\pgfmathresult:3cm);
		%
		\draw[red,thick] (initial) -- (final);
		\draw[cyan,thin] (0,0) -- (initial);
		\stepcounter{c}
	}
	\node[blue,above] at (0:3.125cm){$n = $\,\them};
	\end{tikzpicture}
	%
	\ifthenelse{\them<100}{
			\newframe
	}{
			\end{animateinline}\relax 	% BREAK
	}
} % END \whiledo...
%
\end{center}
\end{frame}
%
%
%
\end{document}